Sorting

The problem of sorting

Problems that become easy once items are in sorted order

• Find a median, or find closest paris
• Binary search, identify statistical outliers

Non-obvious applications

• Data compression: sorting finds duplicates
• Computer graphics: rendering scenes front to back

Insertion sort

Running time: O(n^2) because O(n^2) compares and O(n^2) swaps e.g. when input is A=[n,…,2,1]

Binary Insertion sort

It will take O(log n) time. However, shifting the elements after insertion will still take O(n) time
Complexity: O(n log n) comparisons, n^2 swaps

Merge soft (Key subroutine: Merge)

If n=1, done(nothing to sort). Otherwise, recursively sort A[1..n/2] and A[n/2+1..n]. “Merge” the two sorted sub-arrays
Running time = O(n) to merge a total of n elements (linear time)

Heap Sort

Sorting Strategy:

• Build Max Heap from unordered array;
• Find maximum element A[l];
• Swap elements A[n] and A[l]; now max element is at the end of the array
• Discard node n from heap(by decrementing heap-size variable)
• New root may violate max heap property, but its children are max heaps. Run max_heapify to fix this
• Go to Step 2 unless heap is empty

Running time After n iterations the Heap is empty every iteration involves a swap and a max_heapify operation; hence it takes O(log n) time. Overall O(n log n)

Data structures

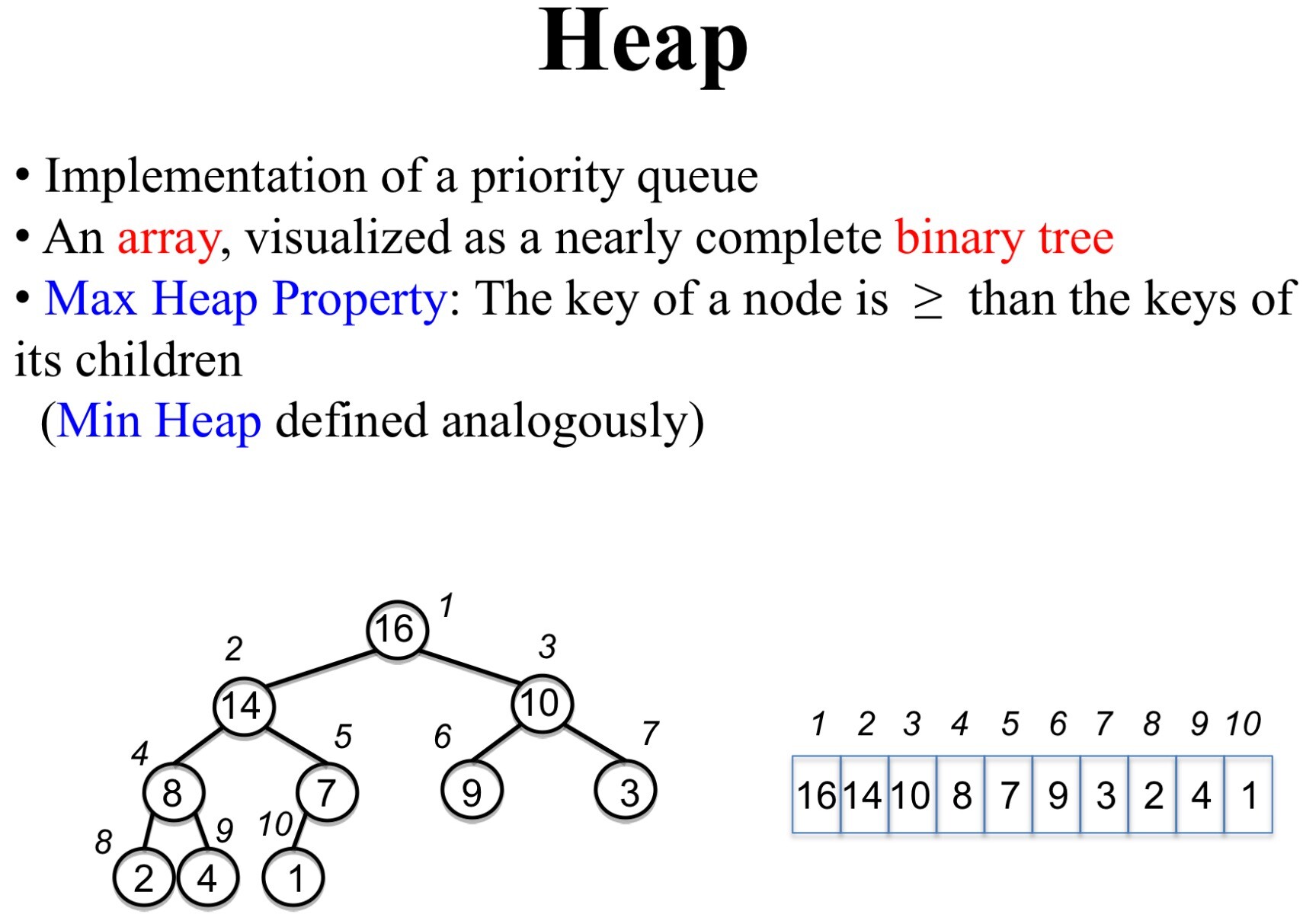
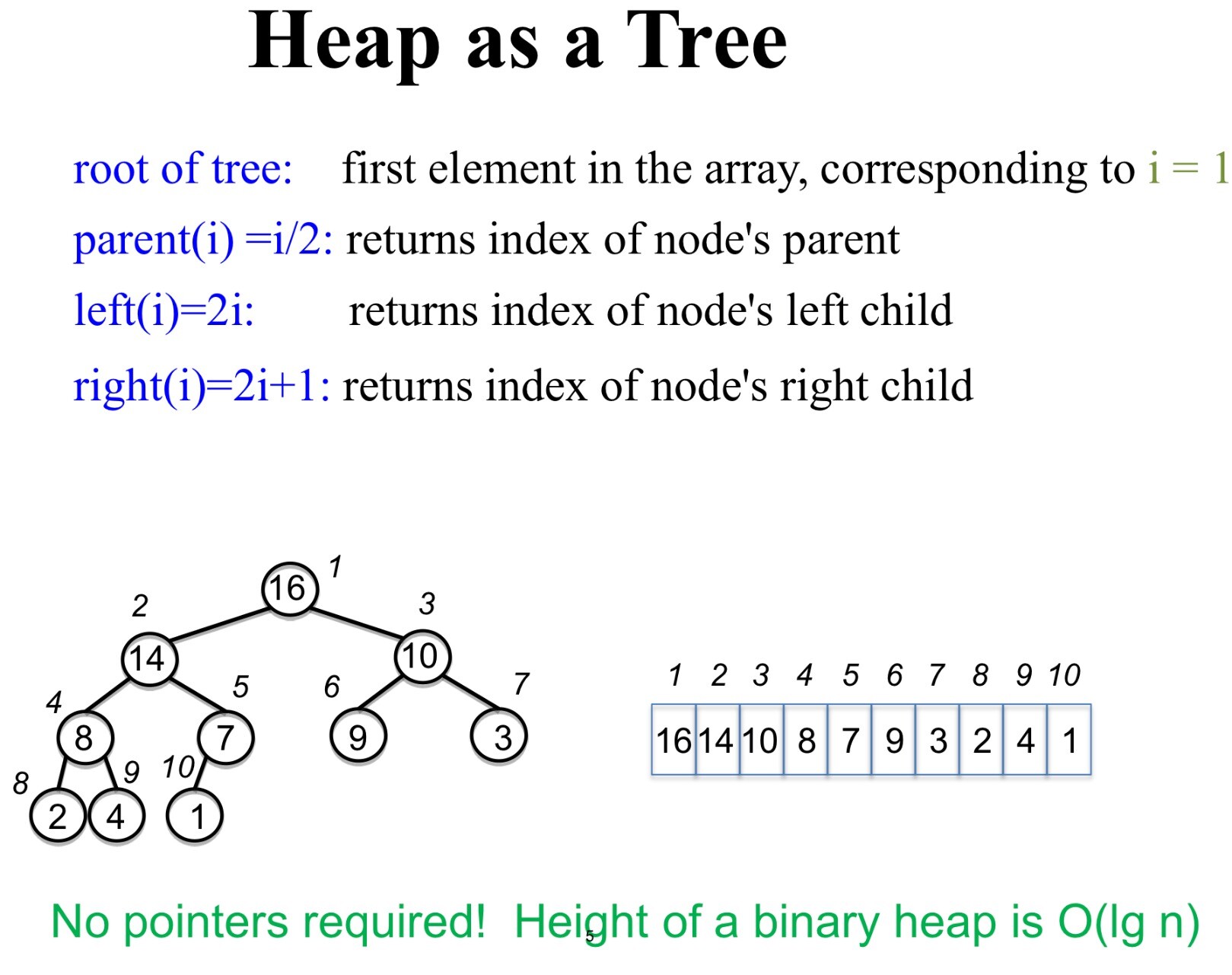
Heap Operations

build_max_help produce a max-heap from an unordered array max_heapify correct a single violation of the heap property in a subtree at its root insert, extract_max, heapsort

Max_heapify with O(log n)

Assume that the trees rooted at left(i) and right(i) are max-heaps

# max_Heapify Pseudocide
l=left(i)
r=right(i)
if(l<=heap_size(A) and A[l]>A[i])
    largest =l
else
    largest=i
if (r<=heap-size(A) and A[r]>A[largest])
    largest=r
if largest !=i:
    exchange A[i] and A[largest]
# Max_Heapify(A, largest)

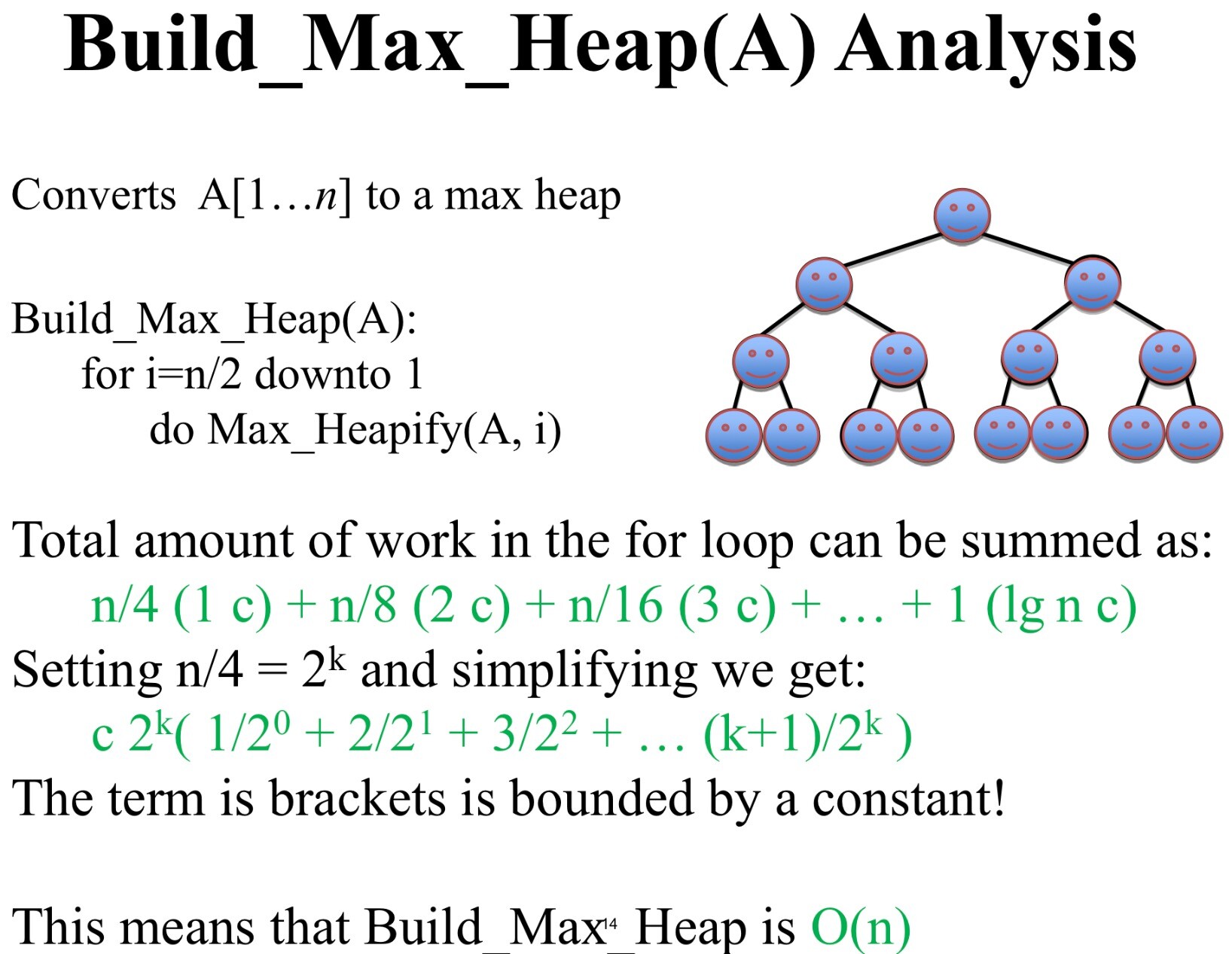
Build_Max_Heap

for i=n/2 down to 1
    do Max_Heapify(A, i)

Source

https://ocw.mit.edu/courses/6-006-introduction-to-algorithms-fall-2011/pages/lecture-notes/