Trees
Scheduling and Binary Search Trees

Binary Search Trees
Properties
Each node x in the binary tree has a key key(x). Node other than the root have a parent p(x). Nodes may have a left child left(x) and/or a right child right(x). These are pointers unlike in a heap.(rooted binary tree)
The invariant is: for any node x, for all nodes y in the left subtree of x, key(y) <=key(x). For all nodes y in the right subtree of x key(y)>=key(x).
Finding a value in the BST if it exists: find(val)
Follow left and right pointers until you find it ot hit NIL
Finding the minimum element in a BST:
Key is to just go left till you cannot go left anymore
Height of node
Length of longest downward path to a leaf
Complexity
All operations are O(h) where h is heigh of the BST, the algorithm for augmentation is as follows:
- Walk down tree to find desired node
- Add in nodes that are smaller
- Add in subtree sizes to the left
# It needs to be implemented with python code
Balanced BSTs
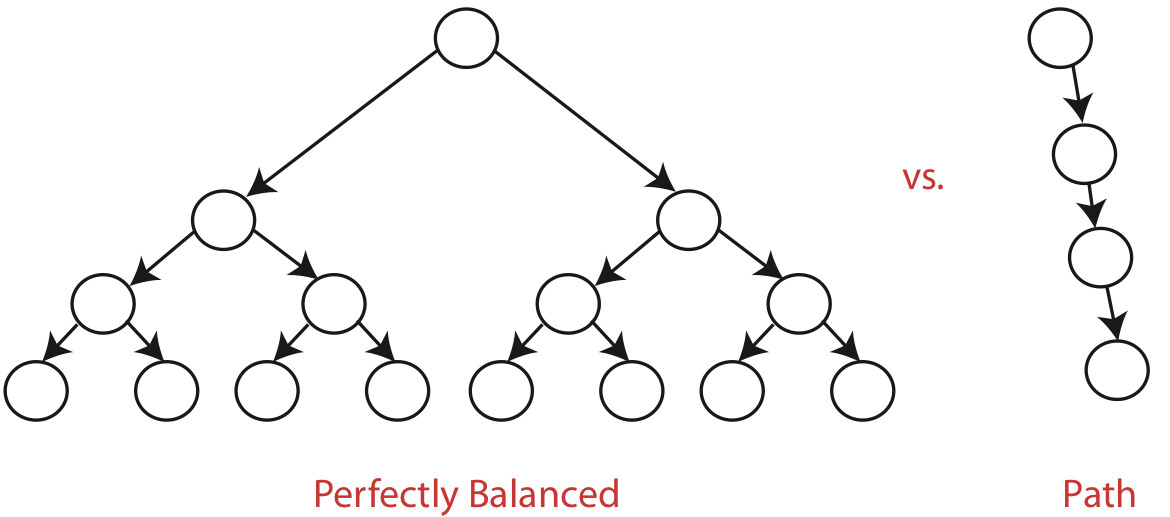
Why the binary search tree needs to be balanced?
- BSTs support insert, delete, min, max,next-larger, next-smaller, etc. in O(h) time, where h =height of tree(= height of root)
- h is between lg n and n
- balanced BST maintains h =O(lg n) -> all operations run in O(lg n) time
AVL Trees
Adel’son-Vel’skii & Landis 1962

For every node, require heights of left & right children to differ by at most +1
- treat nil tree as height -1
- each node stores its height (DATA STRUCTURE AUGMENTATION) (like subtree size)(alternatively, can just store difference in heights)

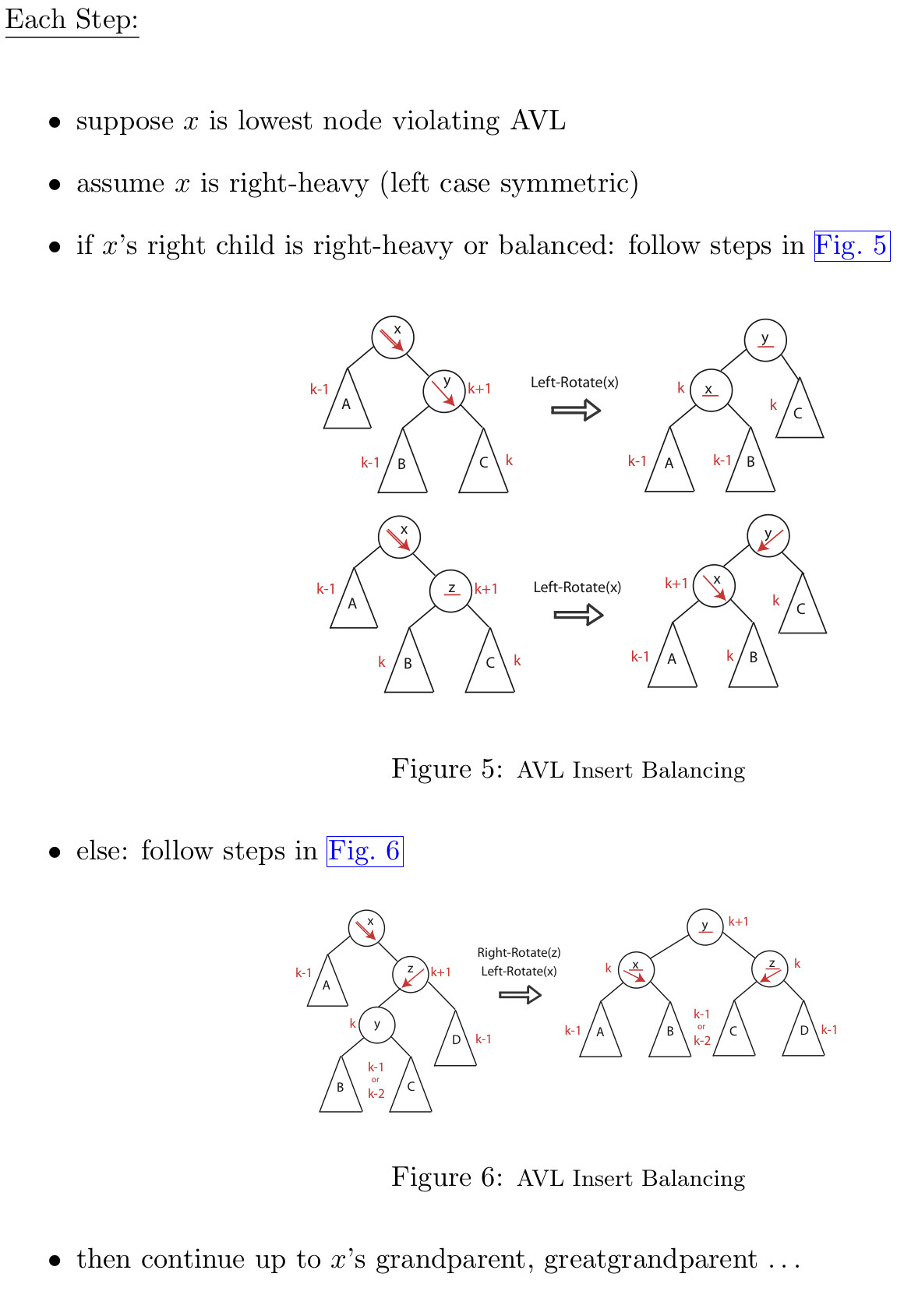
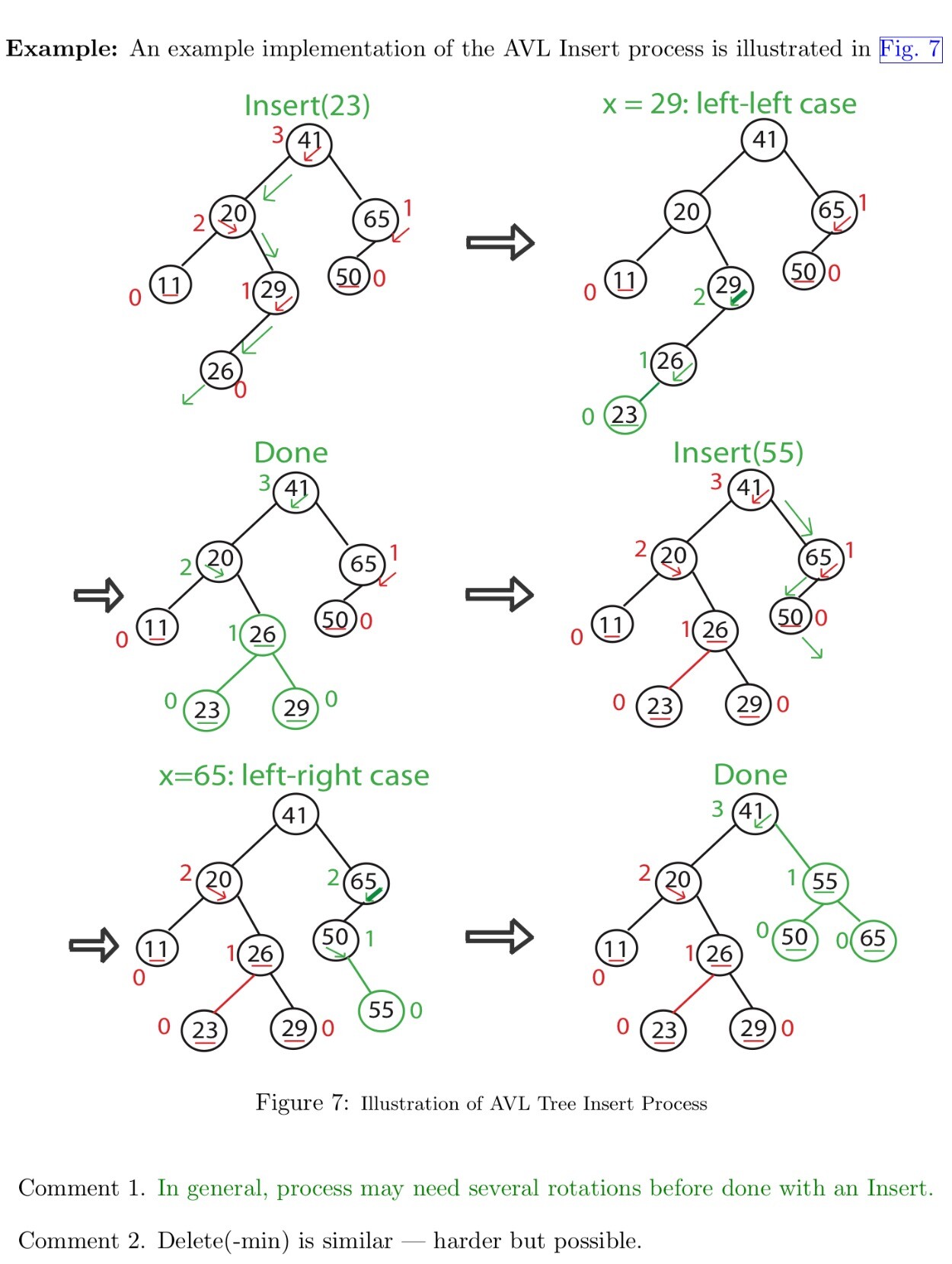
AVL Insert
- Insert as in simple BST
- work your way up tree, restoring AVL property(And updating heights as you go)

Big Picture
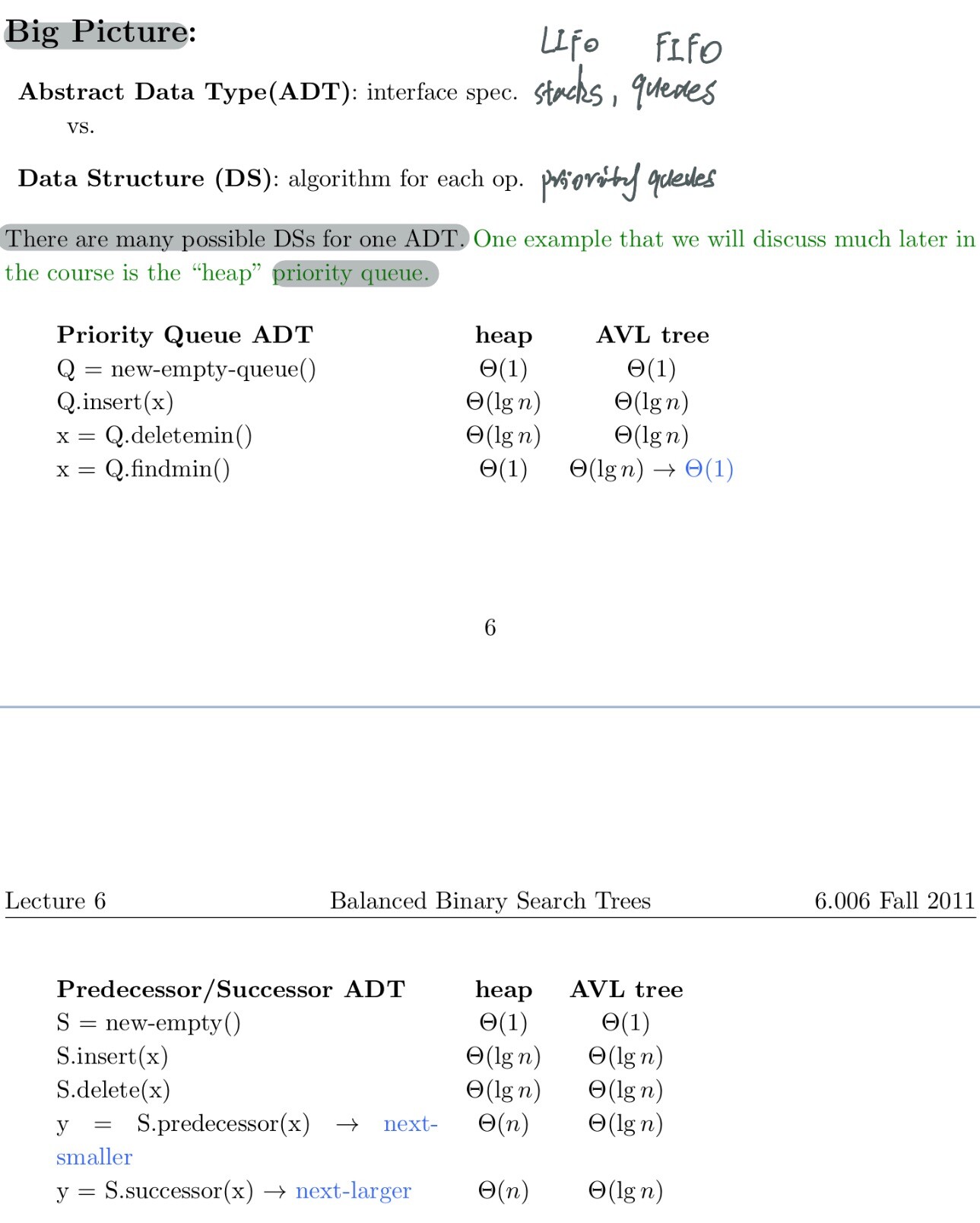
Abstract Data Type(ADT): interface spec
vs
Data Structure(DS): algorithm for each op
There are many possible DSs for one ADT.
Source
https://ocw.mit.edu/courses/6-006-introduction-to-algorithms-fall-2011/pages/lecture-notes/