Sorting Problems

Linear-Time Sorting Overview

• Comparison model
• Lower bounds in the comparison model
  • searching: binary search, AVL tree search optimal

    $$\Omega(lg n)$$
    

  • sorting: merge sort, heap sort, AVL sort optimal

    $$\Omega(n lg n)$$
    

• O(n) sorting algorithms for small integers
  • counting sort
  • radix sort

Comparison Model of Computation

• input items are ADTs
• only support comparisons(<,>,<=, etc)
• time cost =# comparisons

Decision Tree

Any comparison algorithm can be viewed/specified as a tree of all possible comparison outcomes&resulting output, for a particular n, e.g: n=3

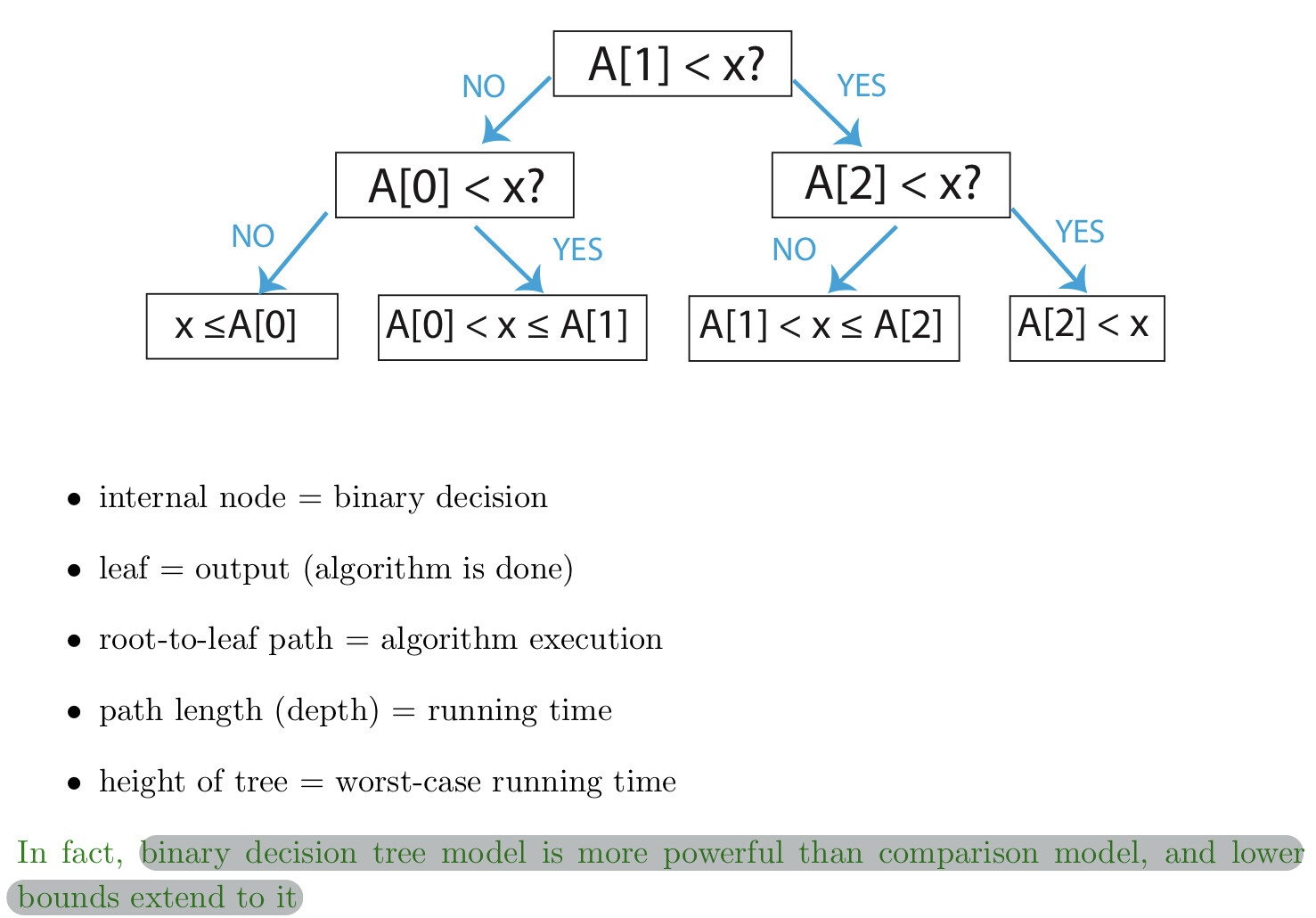
Search Lower Bound

• # leaves >= # possible answers >=n
• decision tree is binary
• ==> height >= \(lgn_{+-\Theta(1)}\)

Sorting Lower bound

• leaf specifies as permutation: A[3]<=A[1]<=A[9]<=…
• all n! are possible answer
• # leaves >=n! ==> \(\\Omega(nlgn)\)

Linear-time Sorting

If n keys are integers, * ==> lower bounds do not apply * if $k=\mathrm{n}^{O(1)}$, can sort in O(n) time

Counting Sort

Time: \(\Theta(n+k)\); also \(\Theta(n+k)\) space

About Radix Soft

Source

https://ocw.mit.edu/courses/6-006-introduction-to-algorithms-fall-2011/pages/lecture-notes/