Data and Signal Processing

Analog signals

Analog data takes on continuous values, measured in hertz(Hz).

• Varies smoothly over time like audio, video, data sampled by sensor

Analog signal can be described as sine wave, it can be in time domain or frequency domain.

• wavelength of a signal is the distance occupied by a single cycle. =v*T
  • (v is the speed of signal)
  • T is distance (the corresponding phase of two consecutive cycles)

Sine wave

Sine wave has different amplitude and frequency

Spectrum

The range of frequency a signal contains, it can be represent by time-domain and frequency-domain with a same vertical axis(amplitude show as v)

Bandwidth(Hz)

The width of the spectrum, bandwidth=(highest frequency - lowest frequency)

Digital Signals

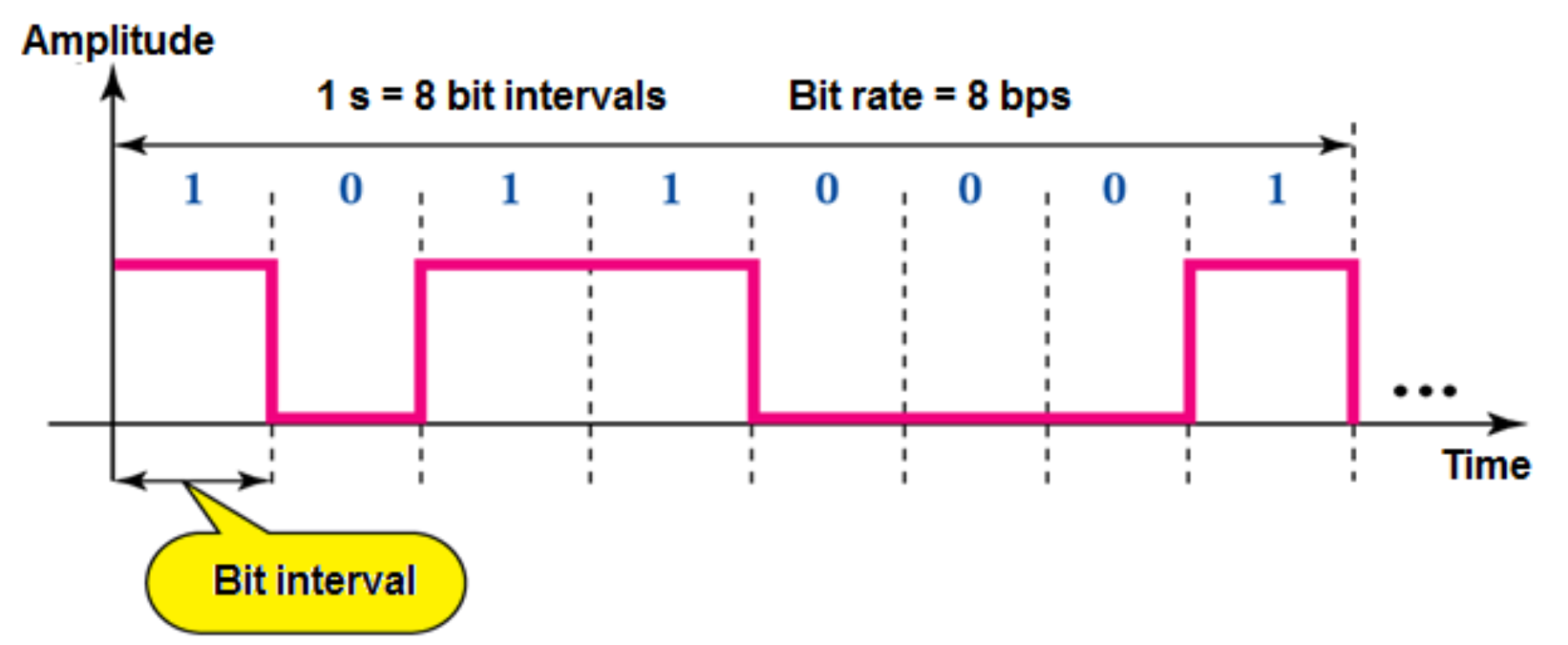
Digital data takes on discrete values, measured in bit per second(bps)

• Maintains a constant level then changes to another constant level, like text integers

Bit interval is the inverse of the bit rate, bit interval=1/(a bit rate) (ms=10^3s us=10^6s)

How to convert an analog signal into digital signal?

It has three steps and was called as A/D Conversion.

Sampling

the input is continuous variable signals(theoretically infinite number of values)
the output is the multi-level digital signals(has defined levels or states)
outputs have levels (levels=2^(bit depth))

Quantization

A process called quantization, it means there is an essentially randomized part of the signal

• Sample analog signal(infinite) in time (horizontal)
• Find closest approximation to a finite set of known values(vertical)

Accuracy depends on sample interval and bit depth.

What is the Quantization codes?

How to calculate the quantization values and quantized error?

The sample’s amplitude value is ons of the decimal range possible value. Decimal range is equal to 2^(bit-depth). E.g: 3 bit-depth have decimal range is 2^3=8

Quantization error=quantized_value - sampled_value

Sampling Theorem

Any transmission system has a limited band of frequencies(bandwidth)
The samples contain all the information of the original signal, if a rate higher than twice the highest signal frequency.

More bandwidth leads to greater costs, limited bandwidth leads to distortion. E.g:

# A 4-kHz bandwidth analog voice signal, each sample requires 8 bits

# We need to sample the signal at twice the highest frequency(based on the sampling theorem)
# bit_rate=2*4000*8=64kbps

# bit depth is reduced to 4, a high quantization error will be incurred. The original signal could not be recovered properly.

# if the bit depth is increased to 16, it requires more storage space and more bandwidth for transmission
# bit_rate=2*4000*16=128kbps

Sample rate(sampling frequency=wave frequency) should be enough

• More wave frequency would be good record high quality(twice is enough, more is good but not useful, we need to balance trade off)

Quantized and Quantization Errors

3 is not enough level for good quality, so will cause error because error was related to quality.

Transmission error

Redundancy for error detection

Parity check

• Even check
• Cyclic redundancy check for big binary
  • CRC polynomial
  • how many bits in reminder? it depends on divisor
  • CRC calculation
  • 7 digit for ASCII code

Encoding

Hamming code

Detection and correction error, the most efficient way of adding parity bits to a set of data bits.

Parity check bits are at position with power of 2. Each parity r bit is the bit for a combination of data bits:

• r1=bits 1,3,5,7,9,11
• r2=bits 2,3,6,7,10,11
• r4=bits 4,5,6,7
• r8=bits 8,9,10,11

Data bit:3,5,6,7,9,10. Parity check bit: 1,2,4,8.

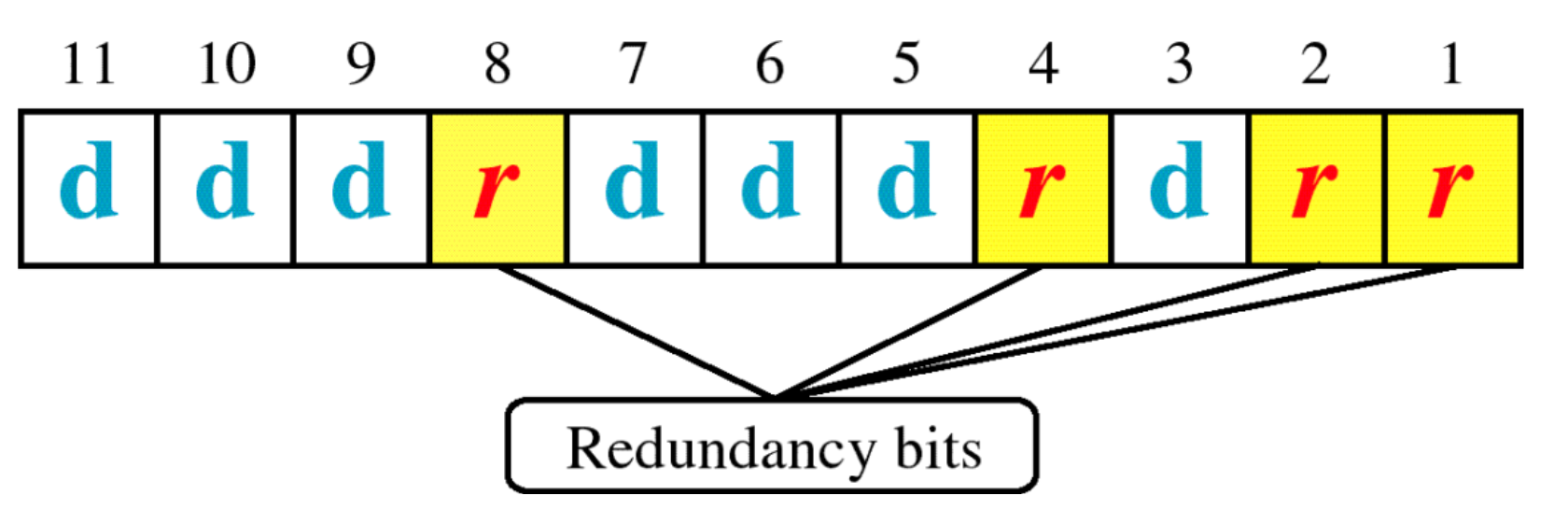
Redundancy Bits Calculation

We can use the calculator.(Actually, we do not know where is the calculator.)